Я с детства любил головоломки и конструкторы в любом их виде, от советских клонов "Лего" (такие были, да), до всяких там скандинавских кроссвордов (которые, как и обычные, мы с батей разгадывали наперегонки в неимоверных количествах).
Оставив место для ностальгии по тем детским увлечениям, я резко перепрыгну во времена учëбы в институте. Программирование я выбрал именно потому, что это головоломка и конструктор в одном флаконе, и по той же причине я любил предметы, также сочетавшие в себе эти свойства.
К примеру, замечательная дискретная математика. Я просто кончал радугой, выводя преобразования всяких конъюнкций и стрелок Пирса (ещё там был штрих Шефнера, но мне не нравилось, как он на меня шипел), строил связные графы и оперировал множествами. Такая-то годнота - и был еë курс мал и короток. Самый базовый уровень, явно недостаточный для подготовки хорошего программиста - по-хорошему, такое надо давать ещё в школе.
Потом было низкоуровневое программирование, здорово вскипятившее мне мозг. Пожалуй, самый лучший курс за всë время - и тоже непростительно куцый. Программирование на ассемблере в реальном режиме под DOS, никакого protected mode или работы с API любых OS. Только-только пошло что-то годное - как курс закончился; зато, блин, как же мы без метрологии или без экономики?
Но самой большой несправедливостью, до сих пор отзывающейся тянущей болью в сердце, является наш курс электротехники.
Электромашины никак не давались мне, и предмет этот был жуткой пыткой. Трëхфазные электродвигатели, сельсины (или синсины? до сих пор не знаю, что это такое), реле и прочий стафф - всë это было не головоломкой и не конструктором, а только грудой мусора, работающего на физических законах, которые яотказывался соблюдать не мог упорядочить и понять. Так что электротехнику я ненавидел до тех пор, пока курс не дошëл до проектирования логических элементов.
О, прекрасные полупроводники! Как только ШМИГИРИЛОВ, ДА-ДА, ИМЕННО В ВЕРХНЕМ РЕГИСТРЕ, рассказал, как на них реализуется любимая мной булева алгебра - я, наконец, осознал, зачем был этот год пыток электричеством! Вот оно - понял я - теперь мы будем проектировать свой процессор, со своей архитектурой, если не аналог 286, то 8080 уж точно! Создадим для него свой набор команд, и собственный ассемблер! Омайгад, как же круто!
Естественно, всë ограничилось лабой на проектирование простеньких сумматоров и мультиплексоров. Одно занятие!
Я разочаровался и ушëл в запой.
Собственно, вся эта портянка была только предисловием. Дело в том, что я тут наткнулся на вот такую штуку: Logisim. Это простой и понятный даже школьнику инструмент проектирования логических схем. И, как гласит его документация, в нормальных учебных заведениях этот софт [зависть]реально используют для учëбы [/зависть]. Я повозился с ним - и мне кажется, что несколько часов работы в этой программе стоят больше всего нашего курса электротехники. Я конкретно залип, начав сначала строить элементарные схемки, вроде тех же сумматоров. Потом, было, дёрнулся собрать что посложнее - и обнаружил, что позабыл все логические правила, как что из чего выводится. Ну это не беда, в сети есть учебники, рассчитанные на читателей любого уровня: я, например, вспоминал основы по этой методичке.
Стоп, тут технически необразованый читатель спросит меня: а, собственно, что это вообще такое вот? Мудоплексоры какие-то, агебра булимическая, одна история лучше другой просто!
Так вот: булева алгебра и логические законы - это, собственно, то, благодаря чему работают все наши компьютеры, телефоны, и прочая цифровая техника.
Благодаря некоторым физическим законам (которые я сейчас понимаю не лучше прежнего) возможно создание полупроводниковых элементов, на которых, в свою очередь, реализуются элементы логические. То есть такие, которые оперируют только понятиями "истина" или "ложь"; в нашем аналоговом мире оказалось очень удобно кодировать эти понятия лепездричеством. Есть напряжение на контакте - "истина" (1), нет - "ложь" (0). Поскольку понятий у нас всего два, то и базовых операций над ними немного - но комбинируя эти базовые операции (реализованные, как раз, логическими элементами), можно вывести всё более сложные; за основами отошлю в вышеуказанную методичку. Суть же в том, что можно задать любое непротиворечивое логическое правило (или их набор), записать его формулой, а по этой формуле построить электрическую схему.
Собственно, вся электронная начинка наших девайсов и состоит из таких схем. Конечно, очень сложных, но, тем не менее: сверхсовременный многоядерный йоба-процессор на этом уровне ничем не отличается от логических машин середины прошлого века. А уж про то, что комбинациями нулей и единичек можно кодировать абсолютно любую информацию - про это я рассказывать не буду, о таком стыдно не знать.
Но хватит теории. Слева я нарисовал простейший полусумматор, реализованный только базовыми элементами - НЕ/И/ИЛИ (инвертор,/конъюнктор/дизъюнктор или, в сишной нотации, !/&/|), - два бита на вход, их сумма в двоичном виде на выходе:

Собранные схемы можно использовать для дальнейшего конструирования. Так, например, из полусумматоров собирается сумматор, оперирующий уже тремя битами (то есть умеющий считать уже от нуля до трёх, а не до двух, как полусумматор):

А вот что показалось мне действительно интересным - так это создать схему, выводящую на восьмисегментный индикатор шестнадцатиричное представление двоичного числа, закодированного в четырёхбитном регистре (четыре бита кодируют числа от 0x0 до 0xF). Индикатор в программу встроен, позиция контактов у него аналогична индикатору TIL321 от Texas Instruments. Восьмой контакт, кстати, не понадобится - он отвечает за сегмент точки, таким образом на входе получается четыре бита, на выходе - семь.
Для начала я сделал таблицу, расписывающую, какие сегменты (R1 - R7) должны гореть при той или иной цифре, а также представление этой цифры в двоичном коде (A,B,C,D):
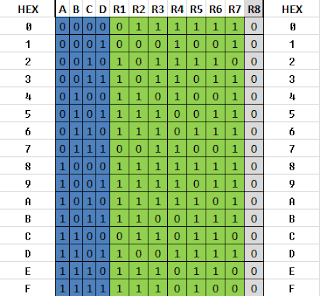
Затем стал выводить правила, реализующие полученную логику. Например, для сегмента R1 полное правило можно записать так (я буду использовать сишную символику, поскольку мне не хочется возиться с привычными мне символами булевой алгебры):
(!A&!B&C&!D)|(!A&!B&C&D)|(!A&B&!C&!D)|(!A&B&!C&D)|(!A&B&C&!D)|(A&!B&!C&!D)|(A&!B&!C&D)|(A&!B&C&!D)|(A&!B&C&D)|(A&B&!C&D)|(A&B&C&!D)|(A&B&C&D)
Это правило вполне рабочее, и уже по нему можно построить схему, которая даже будет включать нужный сегмент:

!A&(!B&C)|B&(!C|!D))|A(!B|B&(C|D))
Если вы дочитали до этого места, сейчас вы ругаетесь. Примерно так: каким это хреном автор выкинул больше половины закорючек?
На самом деле я выкинул все промежуточные приведения и расчёты - а их там на несколько страниц, если с подробностями, которые вам тут совершенно неинтересно будет читать (а мне лениво писать) Поначалу я себе так и расписывал, тратя по несколько часов на одно правило. Потом, когда запомнил законы - стал пропускать промежуточные записи, тратя минут по десять на правило. А потом совсем научился, и стал записывать правило, просто глядя на таблицу; в этом действительно нет ничего сложного, если уметь в логику.
Итак, по сокращённому правилу получается такая схема:

Причём, благодаря всё тем же логическим законам, схема может быть и такой (количество элементов одно, а контакты разные), они полностью эквивалентны:

Но не суть.
В итоге, потратив некоторое время (если честно, меня так увлёк процесс, что я даже не мог заснуть), я нарисовал схему полностью:
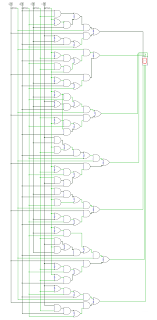


Файл со схемой можно загрузить по ссылке.
Следующая задача - смоделировать простенький процессор. Тут в самом деле нет ничего сложного, самый простой четырёхбитный процессор будет сложнее только в два-три раза. Затем можно пытаться добавить к нему память, ввод, вывод, в общем - реализовать архитектуру фон Неймана. Но всё это - если не перегорю.
Поскольку мой блог читают, в основном, люди с техническим образованием и Констпаус, думаю, что это было интересно.
Оставив место для ностальгии по тем детским увлечениям, я резко перепрыгну во времена учëбы в институте. Программирование я выбрал именно потому, что это головоломка и конструктор в одном флаконе, и по той же причине я любил предметы, также сочетавшие в себе эти свойства.
К примеру, замечательная дискретная математика. Я просто кончал радугой, выводя преобразования всяких конъюнкций и стрелок Пирса (ещё там был штрих Шефнера, но мне не нравилось, как он на меня шипел), строил связные графы и оперировал множествами. Такая-то годнота - и был еë курс мал и короток. Самый базовый уровень, явно недостаточный для подготовки хорошего программиста - по-хорошему, такое надо давать ещё в школе.
Потом было низкоуровневое программирование, здорово вскипятившее мне мозг. Пожалуй, самый лучший курс за всë время - и тоже непростительно куцый. Программирование на ассемблере в реальном режиме под DOS, никакого protected mode или работы с API любых OS. Только-только пошло что-то годное - как курс закончился; зато, блин, как же мы без метрологии или без экономики?
Но самой большой несправедливостью, до сих пор отзывающейся тянущей болью в сердце, является наш курс электротехники.
Электромашины никак не давались мне, и предмет этот был жуткой пыткой. Трëхфазные электродвигатели, сельсины (или синсины? до сих пор не знаю, что это такое), реле и прочий стафф - всë это было не головоломкой и не конструктором, а только грудой мусора, работающего на физических законах, которые я
О, прекрасные полупроводники! Как только ШМИГИРИЛОВ, ДА-ДА, ИМЕННО В ВЕРХНЕМ РЕГИСТРЕ, рассказал, как на них реализуется любимая мной булева алгебра - я, наконец, осознал, зачем был этот год пыток электричеством! Вот оно - понял я - теперь мы будем проектировать свой процессор, со своей архитектурой, если не аналог 286, то 8080 уж точно! Создадим для него свой набор команд, и собственный ассемблер! Омайгад, как же круто!
Естественно, всë ограничилось лабой на проектирование простеньких сумматоров и мультиплексоров. Одно занятие!
Я разочаровался и ушëл в запой.
Собственно, вся эта портянка была только предисловием. Дело в том, что я тут наткнулся на вот такую штуку: Logisim. Это простой и понятный даже школьнику инструмент проектирования логических схем. И, как гласит его документация, в нормальных учебных заведениях этот софт [зависть]реально используют для учëбы [/зависть]. Я повозился с ним - и мне кажется, что несколько часов работы в этой программе стоят больше всего нашего курса электротехники. Я конкретно залип, начав сначала строить элементарные схемки, вроде тех же сумматоров. Потом, было, дёрнулся собрать что посложнее - и обнаружил, что позабыл все логические правила, как что из чего выводится. Ну это не беда, в сети есть учебники, рассчитанные на читателей любого уровня: я, например, вспоминал основы по этой методичке.
Стоп, тут технически необразованый читатель спросит меня: а, собственно, что это вообще такое вот? Мудоплексоры какие-то, агебра булимическая, одна история лучше другой просто!
Так вот: булева алгебра и логические законы - это, собственно, то, благодаря чему работают все наши компьютеры, телефоны, и прочая цифровая техника.
Благодаря некоторым физическим законам (которые я сейчас понимаю не лучше прежнего) возможно создание полупроводниковых элементов, на которых, в свою очередь, реализуются элементы логические. То есть такие, которые оперируют только понятиями "истина" или "ложь"; в нашем аналоговом мире оказалось очень удобно кодировать эти понятия лепездричеством. Есть напряжение на контакте - "истина" (1), нет - "ложь" (0). Поскольку понятий у нас всего два, то и базовых операций над ними немного - но комбинируя эти базовые операции (реализованные, как раз, логическими элементами), можно вывести всё более сложные; за основами отошлю в вышеуказанную методичку. Суть же в том, что можно задать любое непротиворечивое логическое правило (или их набор), записать его формулой, а по этой формуле построить электрическую схему.
Собственно, вся электронная начинка наших девайсов и состоит из таких схем. Конечно, очень сложных, но, тем не менее: сверхсовременный многоядерный йоба-процессор на этом уровне ничем не отличается от логических машин середины прошлого века. А уж про то, что комбинациями нулей и единичек можно кодировать абсолютно любую информацию - про это я рассказывать не буду, о таком стыдно не знать.
Но хватит теории. Слева я нарисовал простейший полусумматор, реализованный только базовыми элементами - НЕ/И/ИЛИ (инвертор,/конъюнктор/дизъюнктор или, в сишной нотации, !/&/|), - два бита на вход, их сумма в двоичном виде на выходе:

Собранные схемы можно использовать для дальнейшего конструирования. Так, например, из полусумматоров собирается сумматор, оперирующий уже тремя битами (то есть умеющий считать уже от нуля до трёх, а не до двух, как полусумматор):

А вот что показалось мне действительно интересным - так это создать схему, выводящую на восьмисегментный индикатор шестнадцатиричное представление двоичного числа, закодированного в четырёхбитном регистре (четыре бита кодируют числа от 0x0 до 0xF). Индикатор в программу встроен, позиция контактов у него аналогична индикатору TIL321 от Texas Instruments. Восьмой контакт, кстати, не понадобится - он отвечает за сегмент точки, таким образом на входе получается четыре бита, на выходе - семь.
Для начала я сделал таблицу, расписывающую, какие сегменты (R1 - R7) должны гореть при той или иной цифре, а также представление этой цифры в двоичном коде (A,B,C,D):

Затем стал выводить правила, реализующие полученную логику. Например, для сегмента R1 полное правило можно записать так (я буду использовать сишную символику, поскольку мне не хочется возиться с привычными мне символами булевой алгебры):
(!A&!B&C&!D)|(!A&!B&C&D)|(!A&B&!C&!D)|(!A&B&!C&D)|(!A&B&C&!D)|(A&!B&!C&!D)|(A&!B&!C&D)|(A&!B&C&!D)|(A&!B&C&D)|(A&B&!C&D)|(A&B&C&!D)|(A&B&C&D)
Это правило вполне рабочее, и уже по нему можно построить схему, которая даже будет включать нужный сегмент:

!A&(!B&C)|B&(!C|!D))|A(!B|B&(C|D))
Если вы дочитали до этого места, сейчас вы ругаетесь. Примерно так: каким это хреном автор выкинул больше половины закорючек?
На самом деле я выкинул все промежуточные приведения и расчёты - а их там на несколько страниц, если с подробностями, которые вам тут совершенно неинтересно будет читать (а мне лениво писать) Поначалу я себе так и расписывал, тратя по несколько часов на одно правило. Потом, когда запомнил законы - стал пропускать промежуточные записи, тратя минут по десять на правило. А потом совсем научился, и стал записывать правило, просто глядя на таблицу; в этом действительно нет ничего сложного, если уметь в логику.
Итак, по сокращённому правилу получается такая схема:

Причём, благодаря всё тем же логическим законам, схема может быть и такой (количество элементов одно, а контакты разные), они полностью эквивалентны:

Но не суть.
В итоге, потратив некоторое время (если честно, меня так увлёк процесс, что я даже не мог заснуть), я нарисовал схему полностью:



Файл со схемой можно загрузить по ссылке.
Следующая задача - смоделировать простенький процессор. Тут в самом деле нет ничего сложного, самый простой четырёхбитный процессор будет сложнее только в два-три раза. Затем можно пытаться добавить к нему память, ввод, вывод, в общем - реализовать архитектуру фон Неймана. Но всё это - если не перегорю.
Поскольку мой блог читают, в основном, люди с техническим образованием и Констпаус, думаю, что это было интересно.

Комментариев нет:
Отправить комментарий